Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды, а четыре другие вершины — на ее основании. Длина стороны основания пирамиды равна 3, высота пирамиды — 2. Найдите площадь S поверхности куба. В ответ запишите значение выражения 25S.
Вычислите 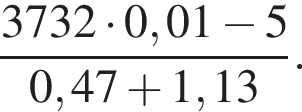
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Основанием пирамиды SABCD является ромб со стороной ![]() и углом BAD, равным
и углом BAD, равным 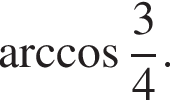 Ребро SD перпендикулярно основанию, а ребро SB образует с основанием угол
Ребро SD перпендикулярно основанию, а ребро SB образует с основанием угол ![]() Найдите радиус R сферы, проходящей через точки A, B, C и середину ребра SB. В ответ запишите значение выражения R2.
Найдите радиус R сферы, проходящей через точки A, B, C и середину ребра SB. В ответ запишите значение выражения R2.
В окружность радиусом 12 вписан треугольник, длины двух сторон которого равны 8 и 12. Найдите длину высоты треугольника, проведенной к его третьей стороне.
Расположите числа 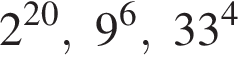 в порядке возрастания.
в порядке возрастания.
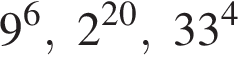
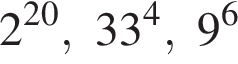
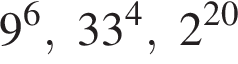
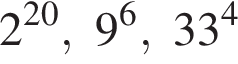
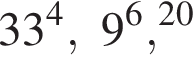
Площадь прямоугольника ABCD равна 55. Точки M, N, P, Q — середины его сторон. Найдите площадь четырехугольника между прямыми AN, BP, CQ, DM.
Если 18% некоторого числа равны 24, то 30% этого числа равны:
Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,9 | |
| b | 108 | 7,6 |
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 102°, ∠BOM = 128°. Найдите величину угла BOC.
Корень уравнения 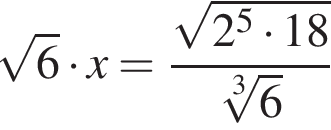 равен:
равен:
Найдите длину средней линии прямоугольной трапеции с острым углом 60°, у которой большая боковая сторона и большее основание равны 10.
Решением неравенства
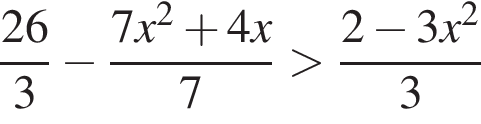
является промежуток:
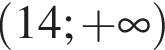 ;
;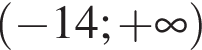 ;
;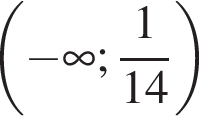 ;
;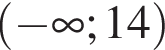 ;
;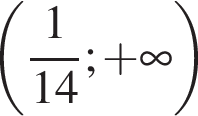 .
.Найдите сумму корней уравнения
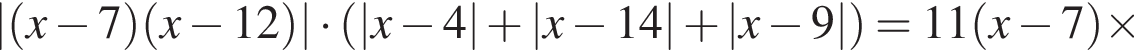
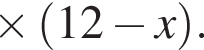
Решите неравенство 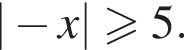
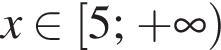


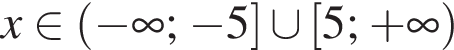
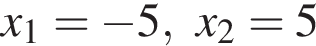
Сократите дробь 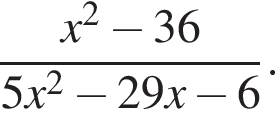
Решите уравнение 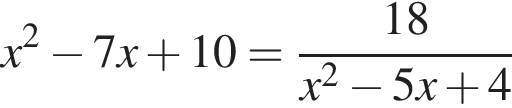 и найдите сумму его корней.
и найдите сумму его корней.
Пусть (x1; y1), (x2; y2) — решения системы уравнений 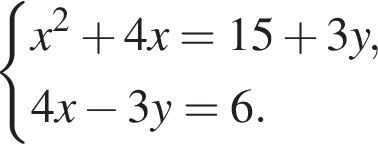
Найдите значение выражения 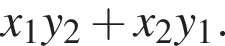
Найдите сумму целых решений (решение, если оно единственное) системы неравенств 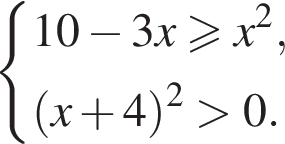
Количество целых решений неравенства 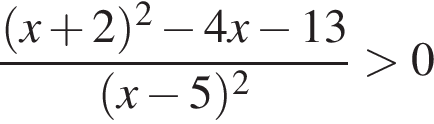 на промежутке
на промежутке 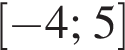 равно:
равно:
Найдите значение выражения 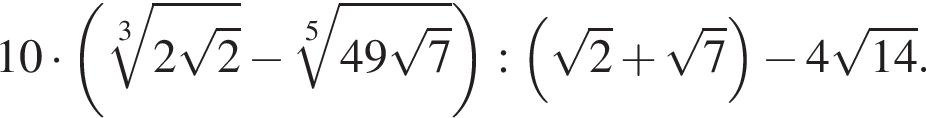
Упростите выражение 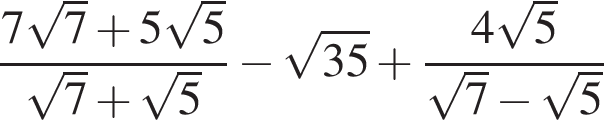
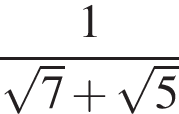
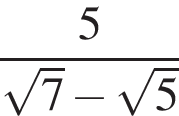
Найдите сумму корней (корень, если он единственный) уравнения 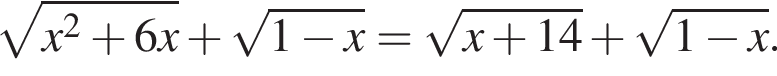
Результат упрощения выражения 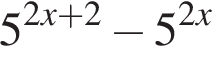 имеет вид:
имеет вид:
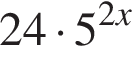
Найдите произведение суммы корней уравнения 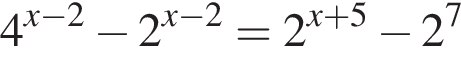 на их количество.
на их количество.
Найдите наибольшее целое решение неравенства 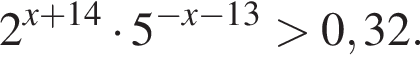
Пусть 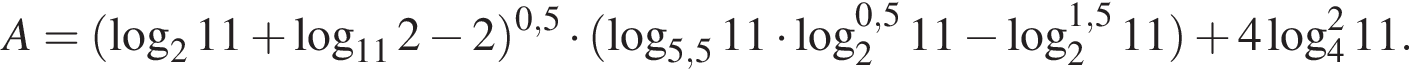
Найдите значение выражения 2A.
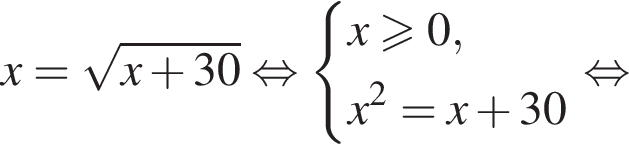
Корень уравнения
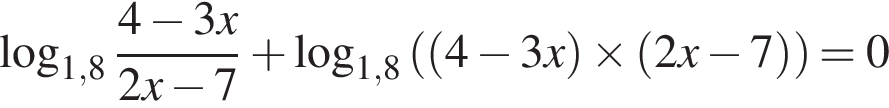
(или сумма корней, если их несколько) принадлежит промежутку:
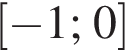
Найдите сумму наименьшего и наибольшего целых решений неравенства 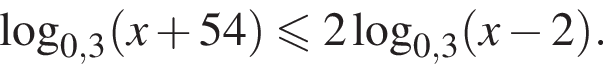
Упростите выражение 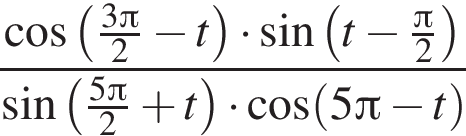
Найдите значение выражения: 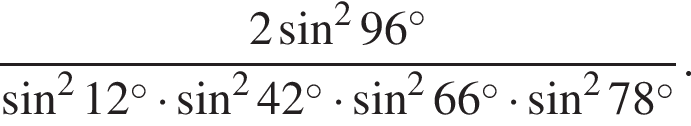
Найдите наименьший положительный корень уравнения 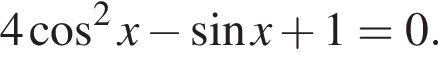

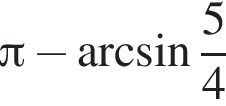
Найдите сумму корней (корень, если он единственный) уравнения 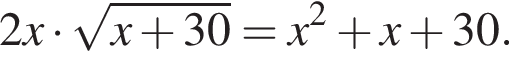
Количество целых решений неравенства 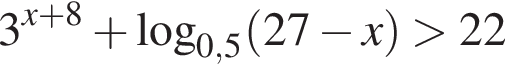 равно ...
равно ...
Геометрическая прогрессия со знаменателем 4 содержит 10 членов. Сумма всех членом прогрессии равна 30. Найдите сумму всех членов прогрессии с четными номерами.
Функция  не определена в точке:
не определена в точке:
Какая из прямых пересекает график функции 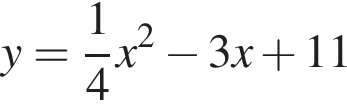 в двух точках?
в двух точках?


На диаграмме показано количество покупателей в период проведения акции в магазине. В какой день количество покупателей товара по акции составило менее 30% от количества всех покупателей в этот день?
На координатной прямой отмечены точки O, A, B, C, D, F.
Если координата точки A равна ![]() то числу 1 на координатной прямой соответствует точка:
то числу 1 на координатной прямой соответствует точка:
Известно, что наименьшее значение функции, заданной формулой y = x2 + 8x + c, равно −5. Тогда значение c равно:
Из пунктов A и B, расстояние между которыми 190 км, одновременно навстречу друг другу выехали два автомобиля с постоянными и неравными скоростями: из пункта A — со скоростью a км/ч, из пункта B — со скоростью b км/ч. Через некоторое время автомобили встретились. Составьте выражение, определяющее расстояние (в километрах) от пункта A до места встречи автомобилей.
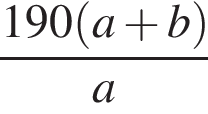
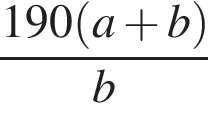
Длины катетов прямоугольного треугольника являются корнями уравнения x2 − 5x + 2 = 0. Найдите площадь треугольника.
Для покраски стен общей площадью 175 м2 планируется закупка краски. Объем и стоимость банок с краской приведены в таблице.
| Объем банки (в литрах) | Стоимость банки с краской (в рублях) |
|---|---|
| 2,5 | 85 000 |
| 10 | 290 000 |
Какую минимальную сумму (в рублях) потратят на покупку необходимого количества краски, если ее расход составляет 0,2 л/м2?
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно точки O.

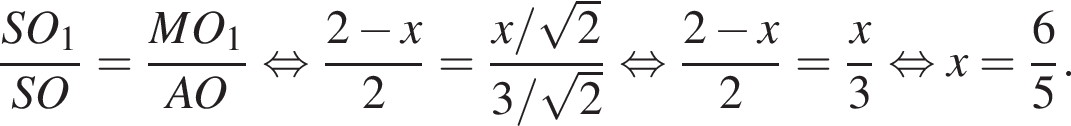
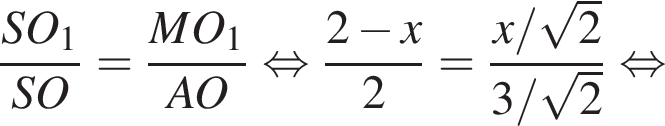
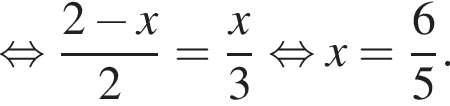
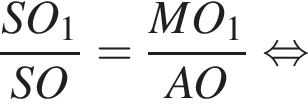
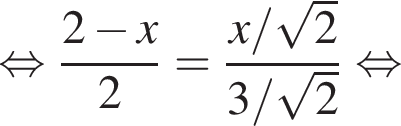
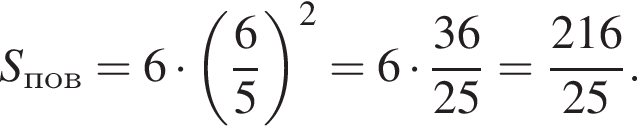
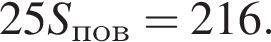
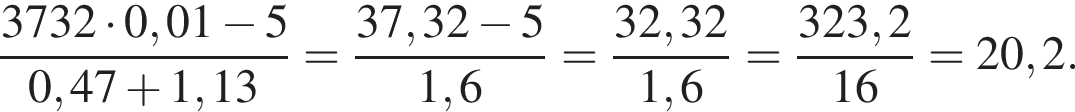
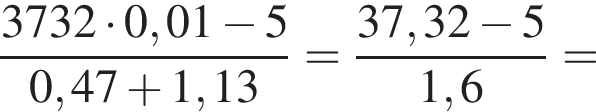
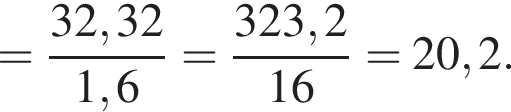
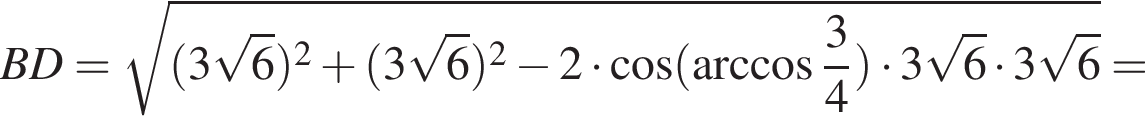

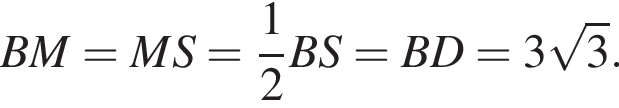
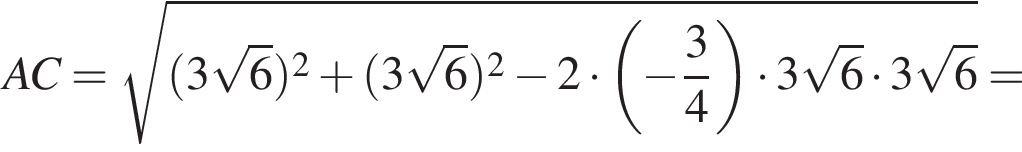
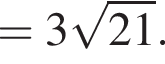
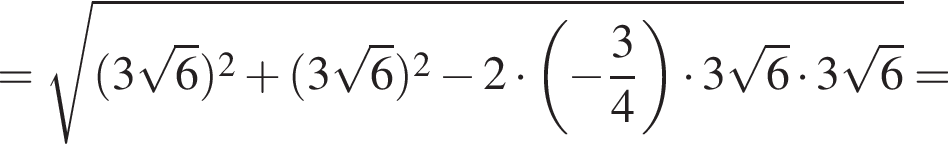
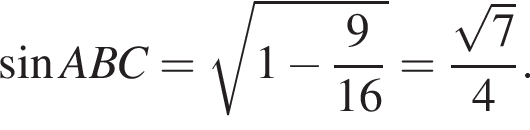
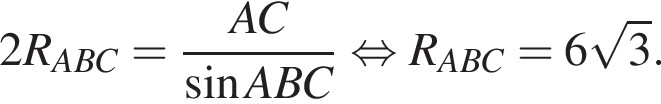
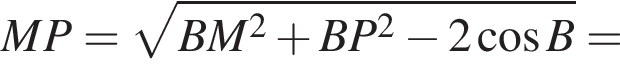
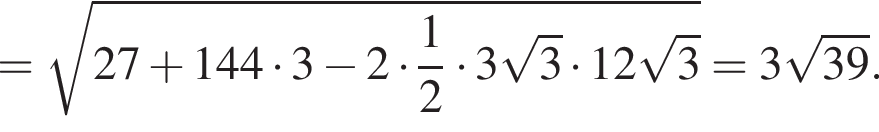
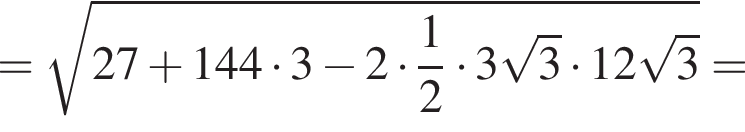


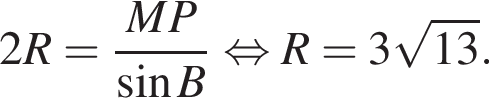 Таким образом,
Таким образом, 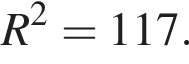
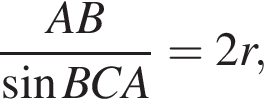 откуда
откуда 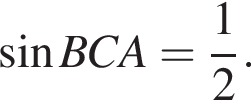 Из прямоугольного треугольника BHC имеем:
Из прямоугольного треугольника BHC имеем: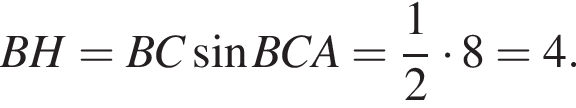
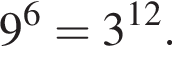 Поскольку все числа положительны, извлечем из каждого корень четвертой степени и получим:
Поскольку все числа положительны, извлечем из каждого корень четвертой степени и получим: 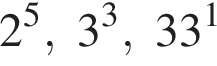 то есть числа 32, 27, 33. Так как 27 < 32 < 33, получаем
то есть числа 32, 27, 33. Так как 27 < 32 < 33, получаем 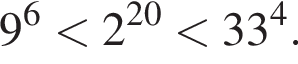
 Поскольку
Поскольку 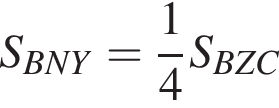 (NY — средняя линия), поэтому
(NY — средняя линия), поэтому 
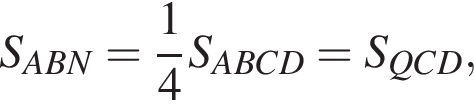 тогда
тогда 

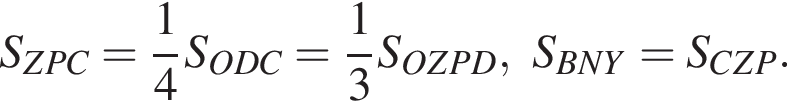
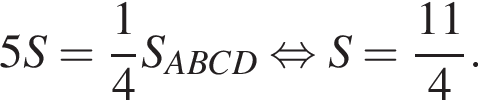
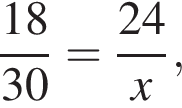 где x — неизвестное число.
где x — неизвестное число.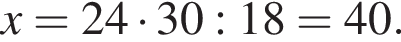

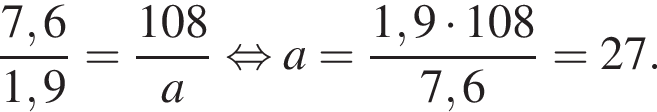
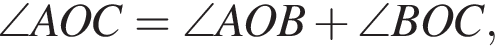
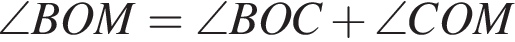 и
и  Таким образом:
Таким образом:
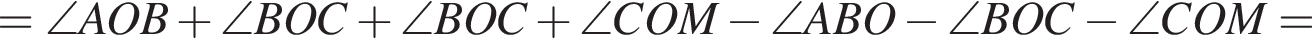
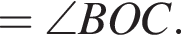
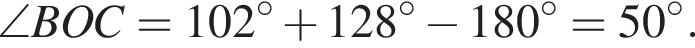
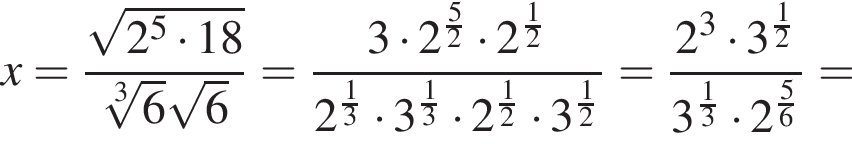
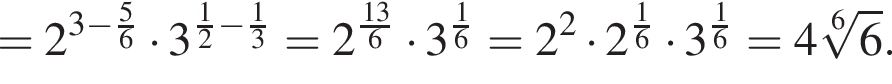
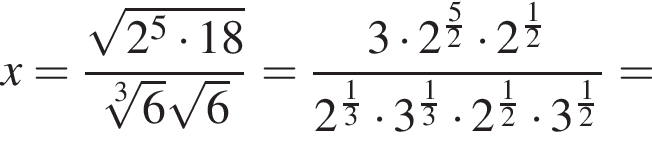
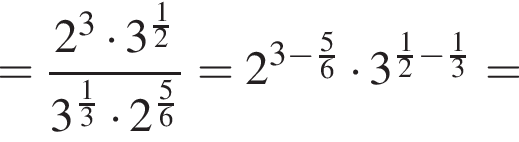
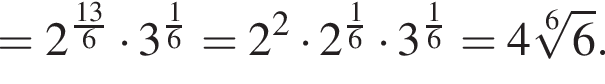
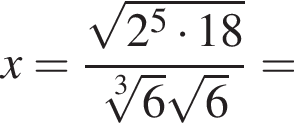
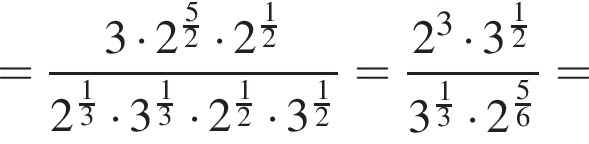
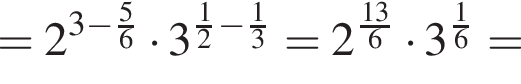
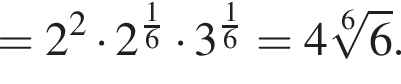
 поэтому
поэтому 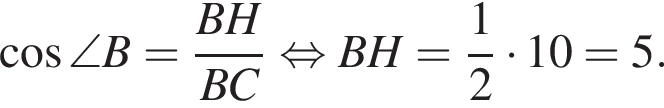 Следовательно,
Следовательно, 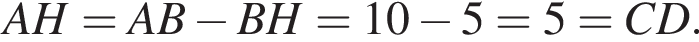
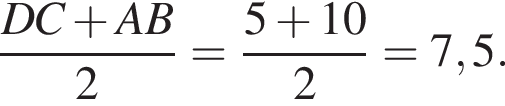
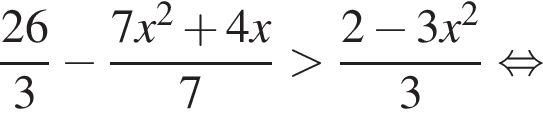
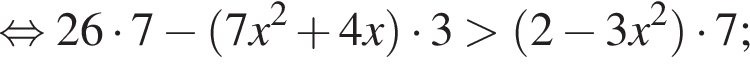
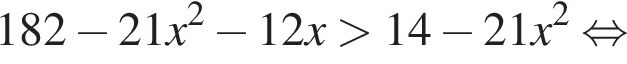

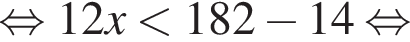

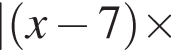
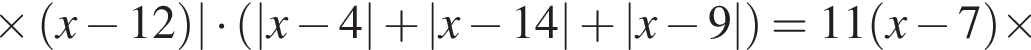
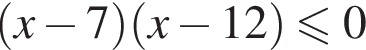 :
: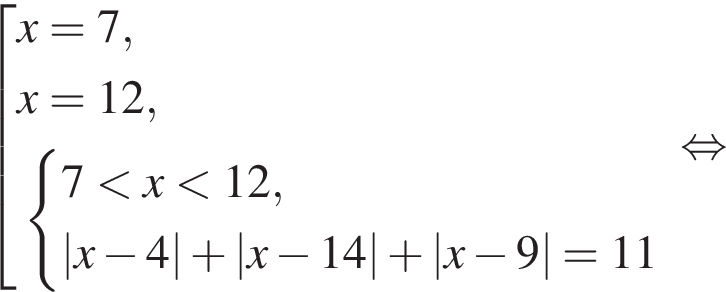
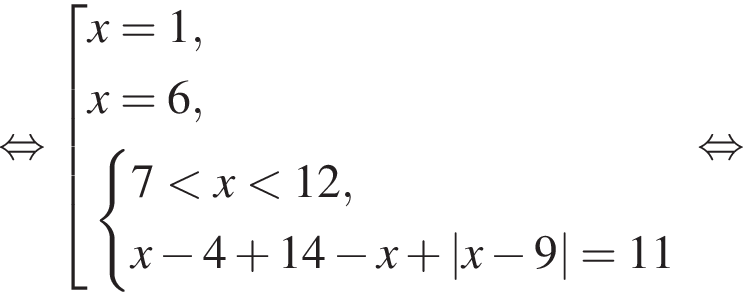
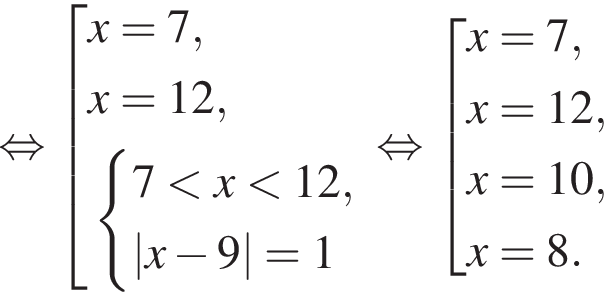

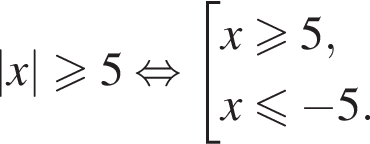
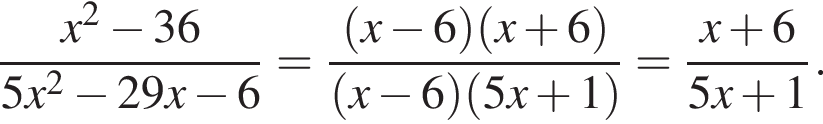
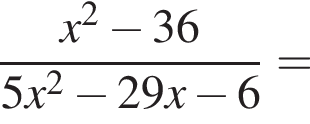
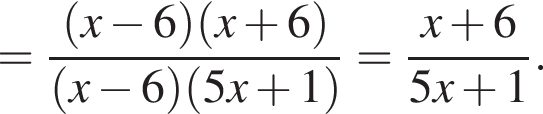
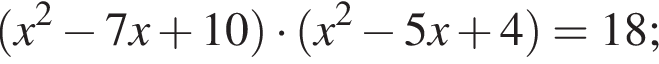


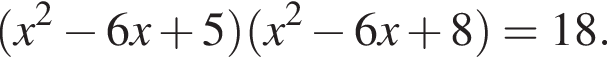
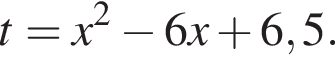 Получим:
Получим: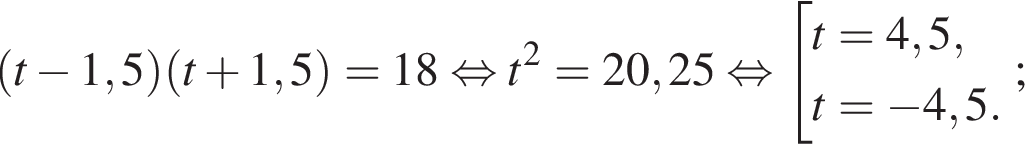
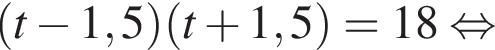
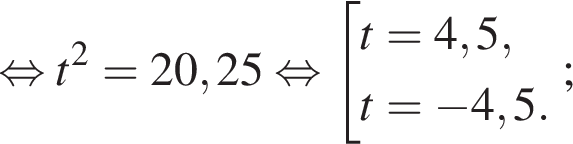
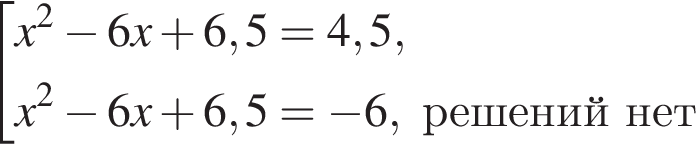
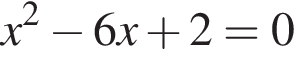 найдем по теореме Виета, она равна 6.
найдем по теореме Виета, она равна 6.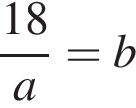 равносильно уравнению
равносильно уравнению  искать ОДЗ не требуется.
искать ОДЗ не требуется.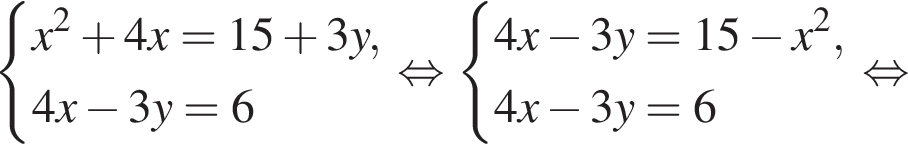
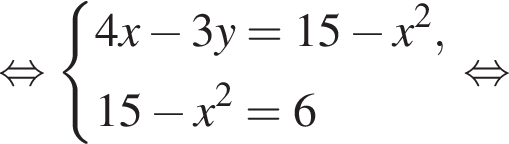
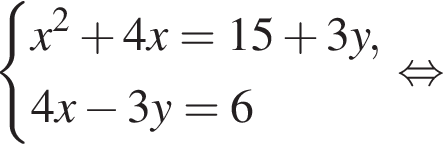
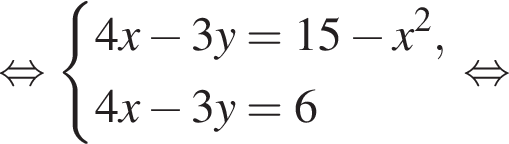
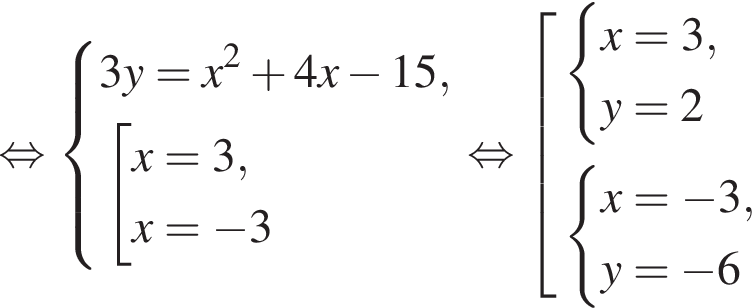


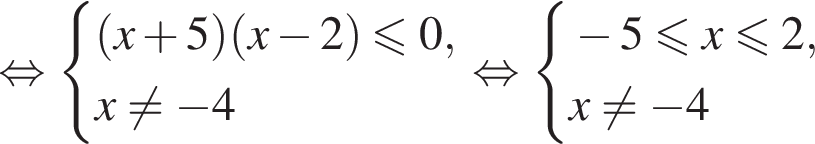
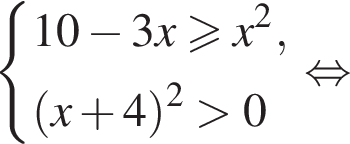
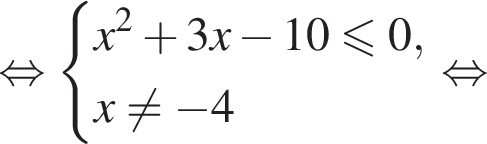
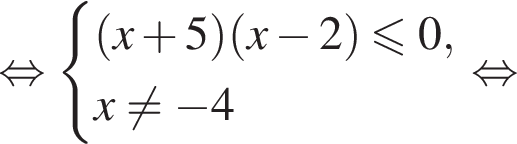
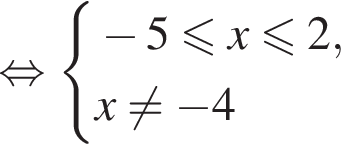
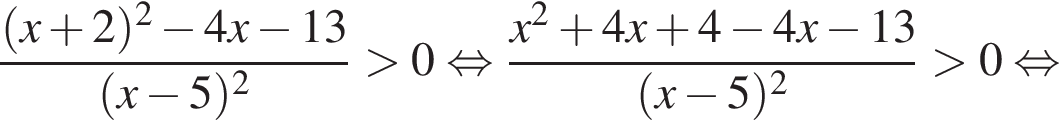
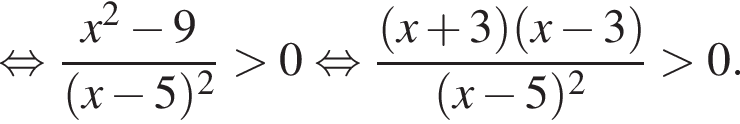
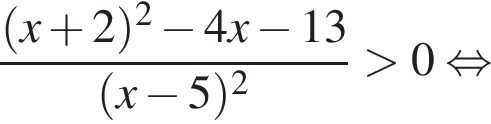
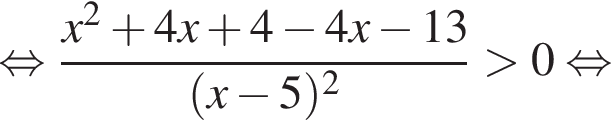
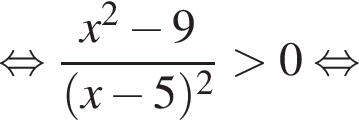
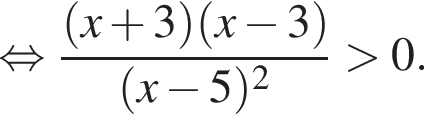
 Корни знаменателя
Корни знаменателя 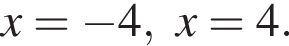 Следовательно, существует только 2 целых решения.
Следовательно, существует только 2 целых решения. 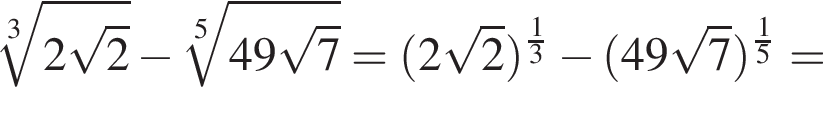
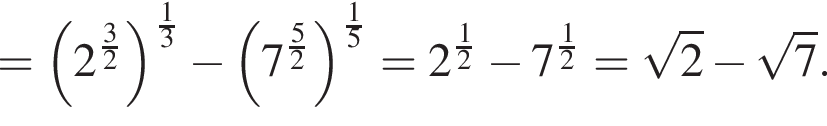
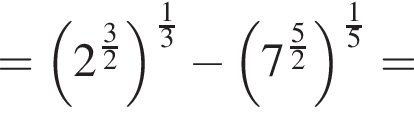
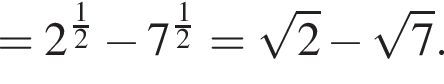
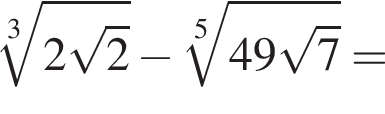
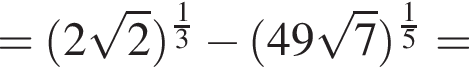
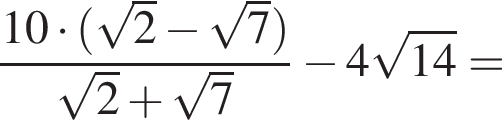
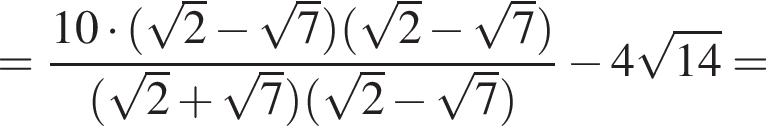
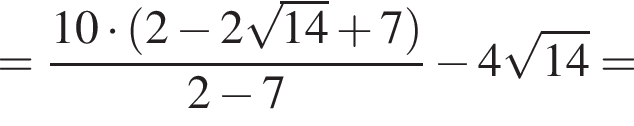
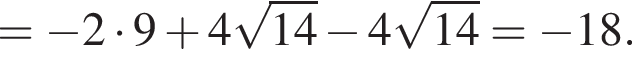
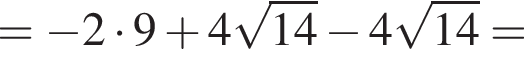
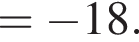
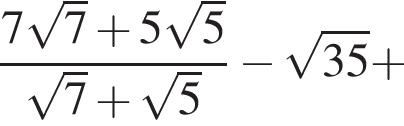
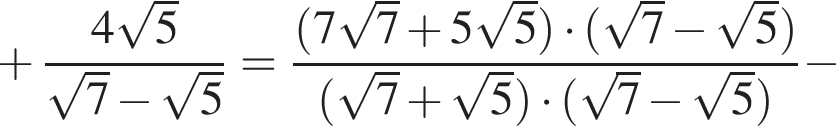
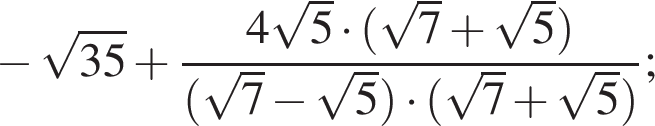

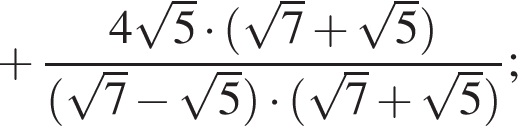
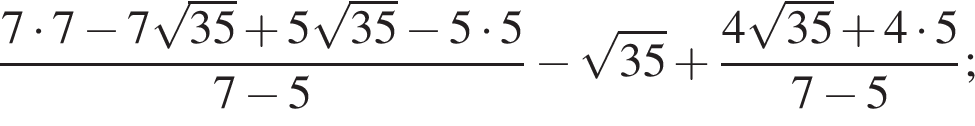
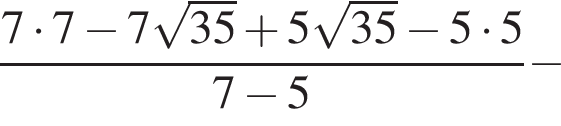
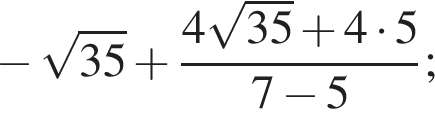
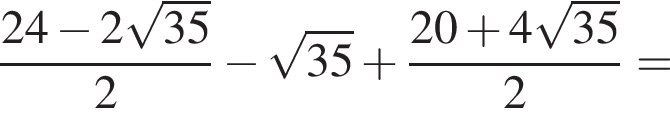
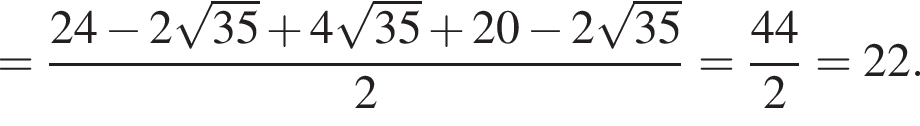
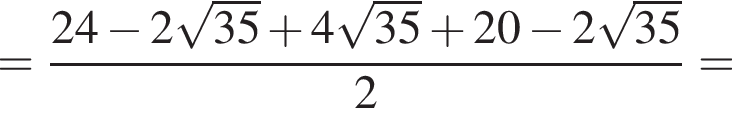
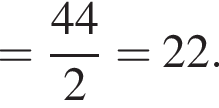
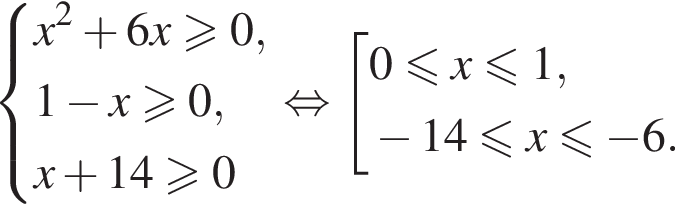
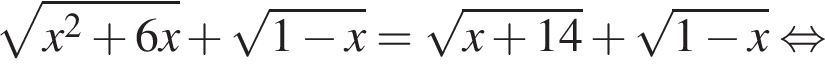
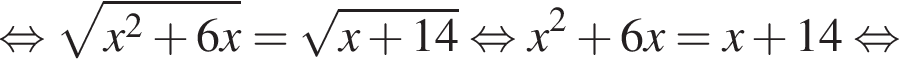
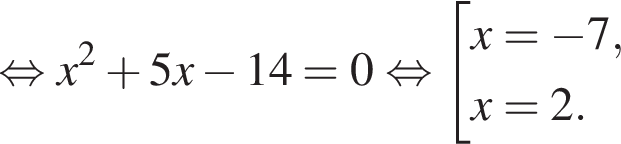
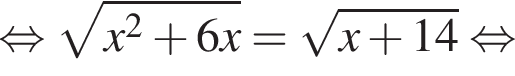
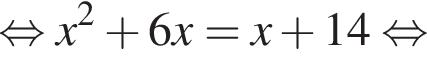
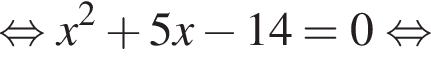
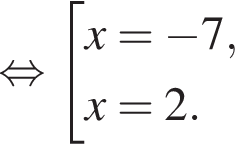
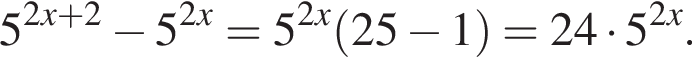
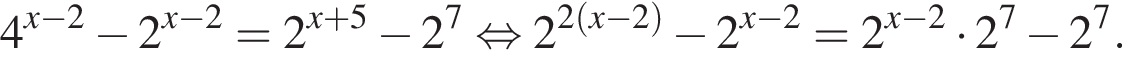
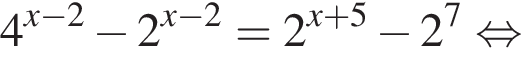
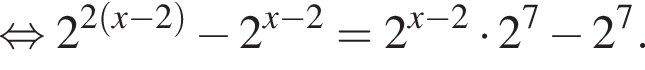
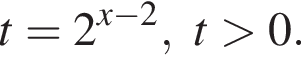 Поэтому:
Поэтому:
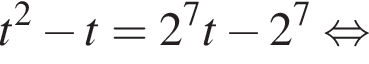
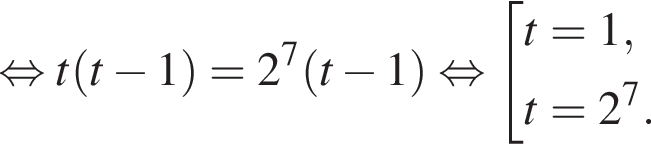
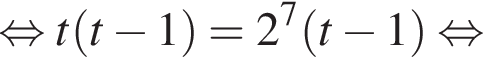
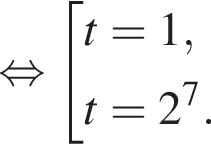
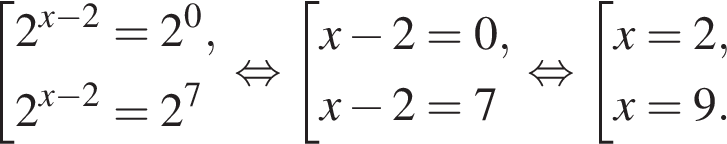
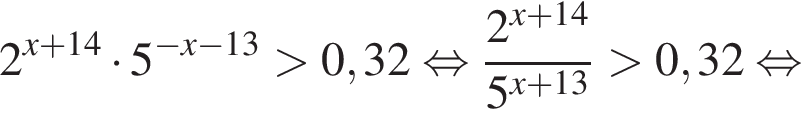
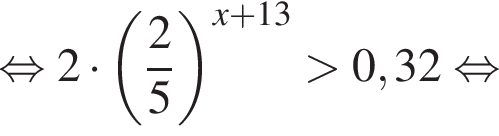
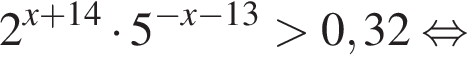
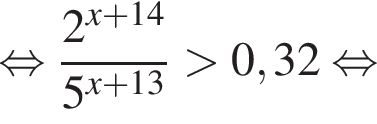
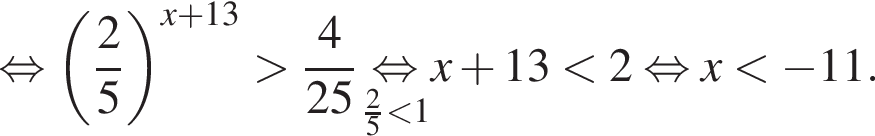
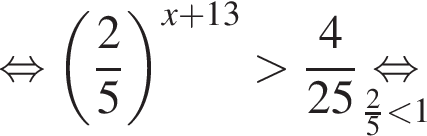
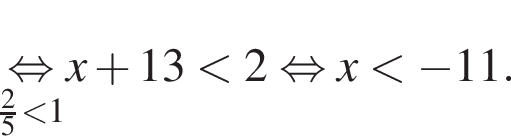
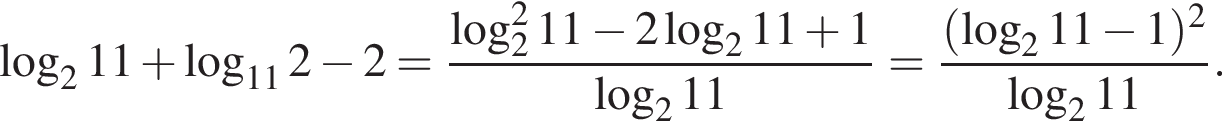
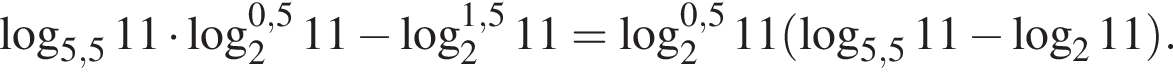
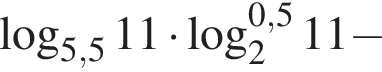

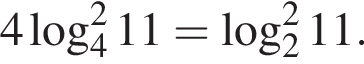 Тогда имеем:
Тогда имеем: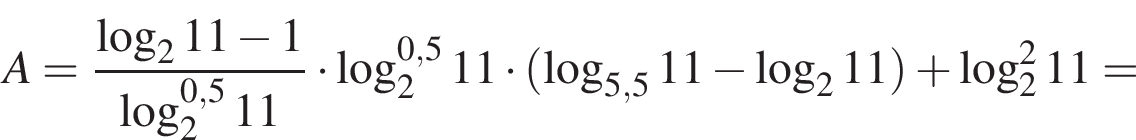
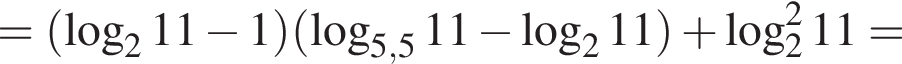
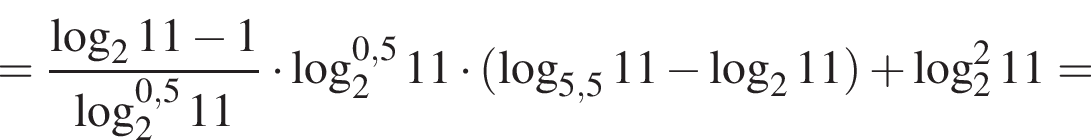
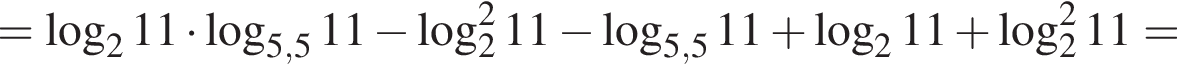
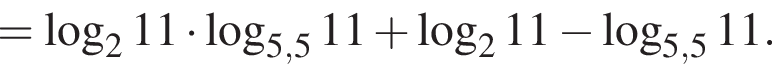
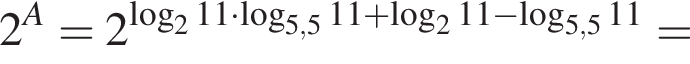
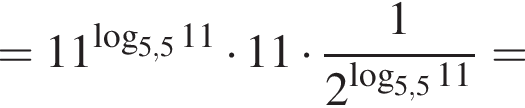
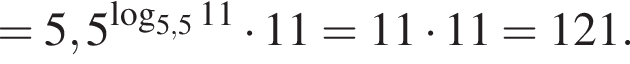
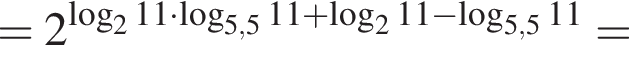
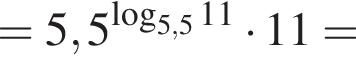
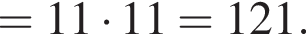
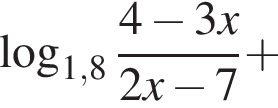
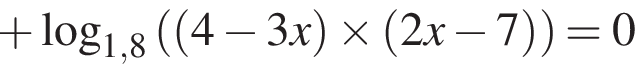
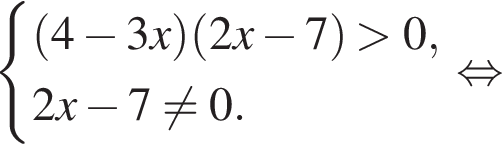
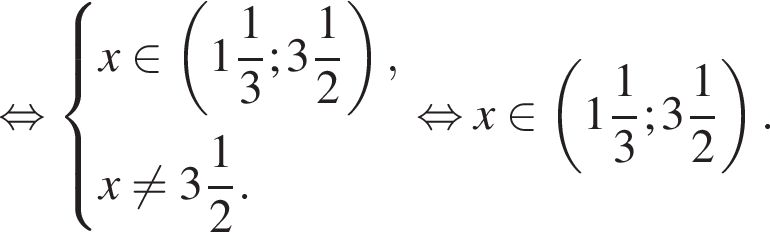
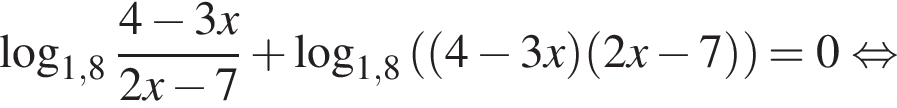
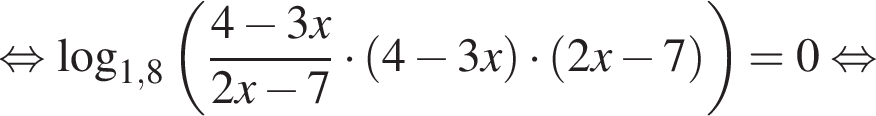
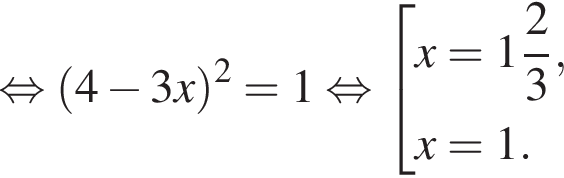
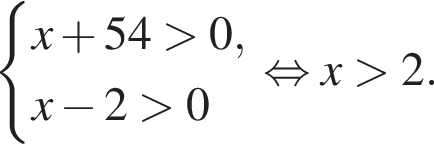
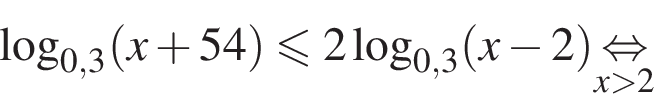
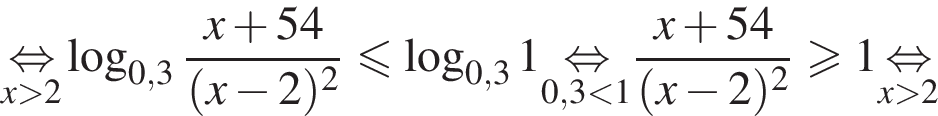
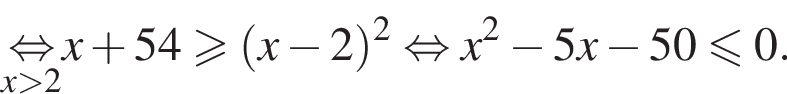
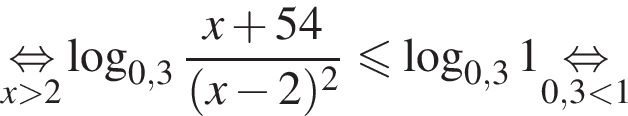
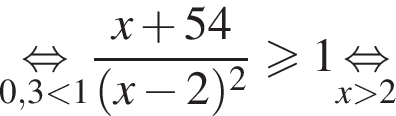

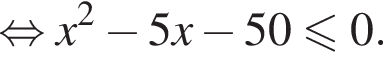
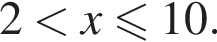 Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.
Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.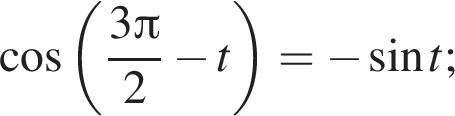
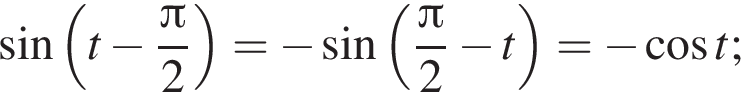
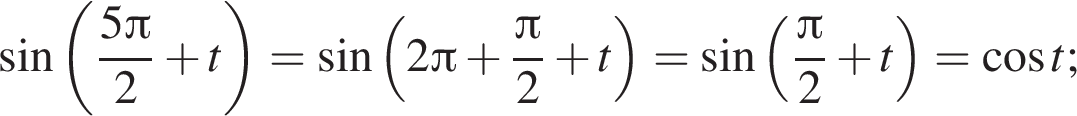
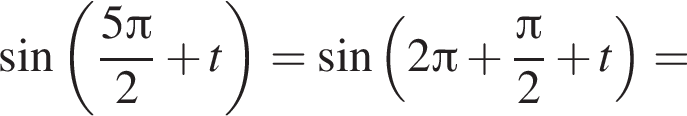
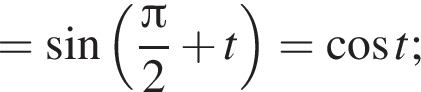
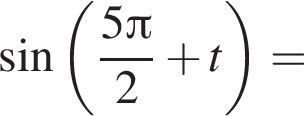
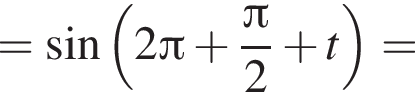
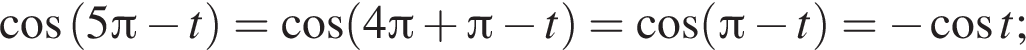

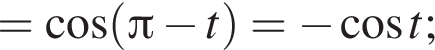
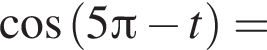
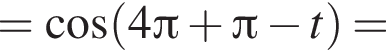
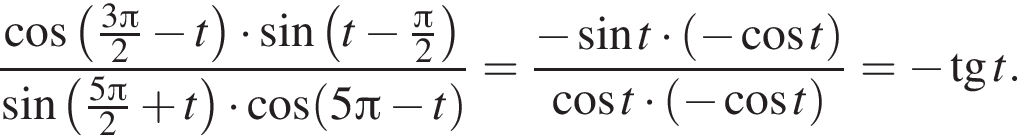
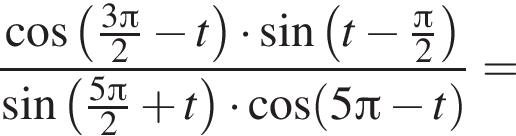
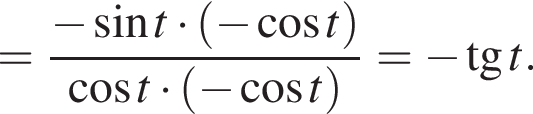

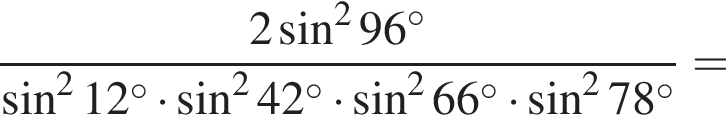
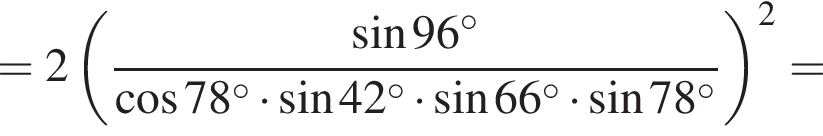
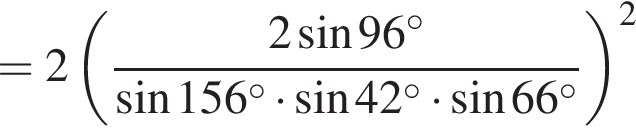
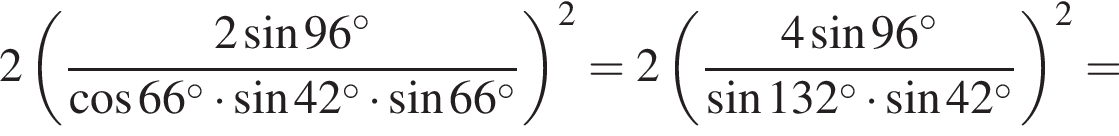
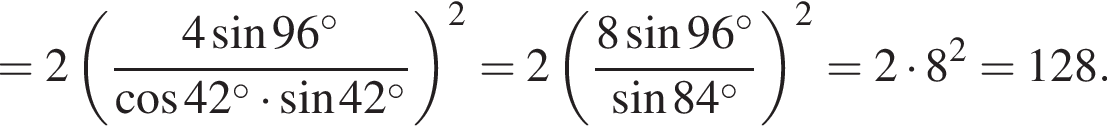
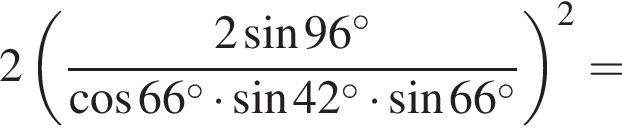
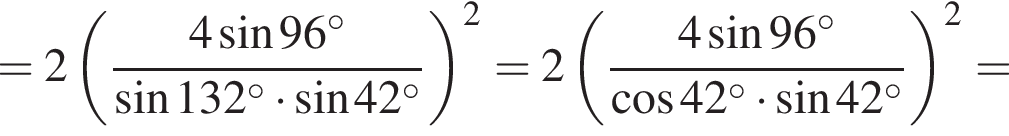
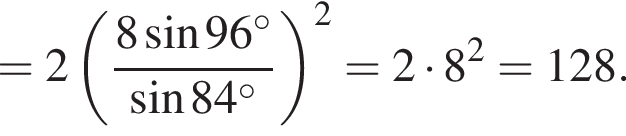
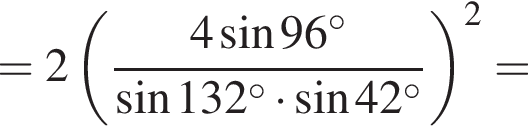
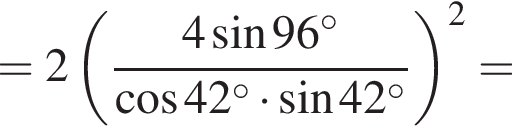
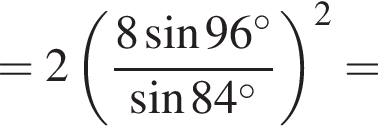
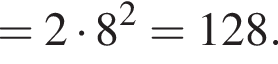
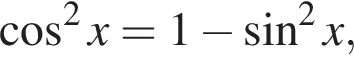 получим:
получим: 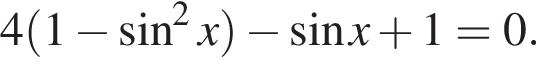 Сделаем замену
Сделаем замену 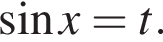 Решим уравнение:
Решим уравнение:
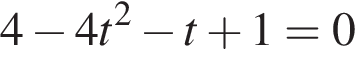
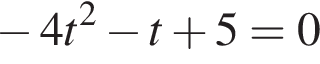
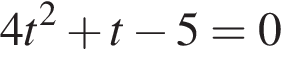
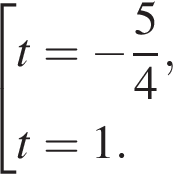
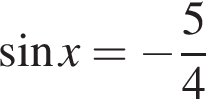 или
или 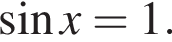 Первое уравнение решений не имеет, поскольку
Первое уравнение решений не имеет, поскольку 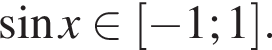 Рассмотрим второе уравнение:
Рассмотрим второе уравнение: 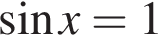
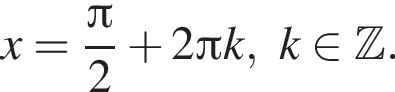
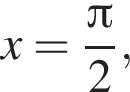 он указан под номером 2.
он указан под номером 2. Тогда:
Тогда: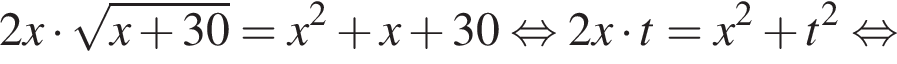

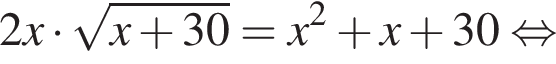


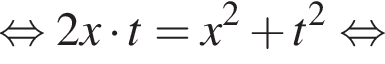
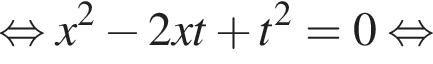
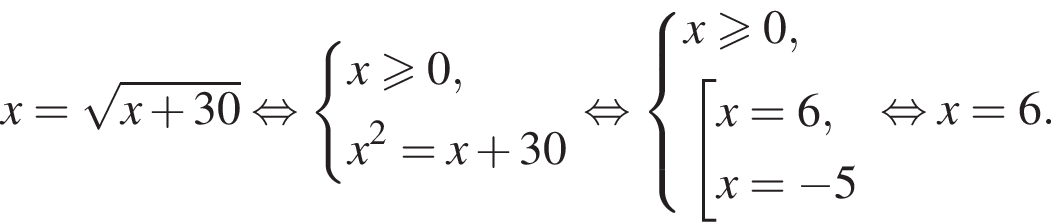
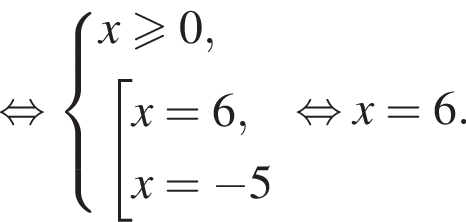
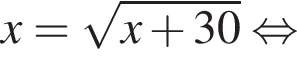
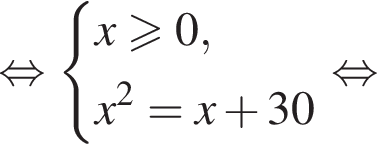
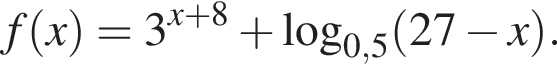 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 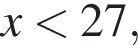 и что на
и что на 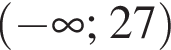
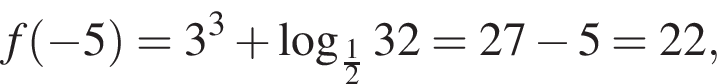 неравенство верно для всех x из
неравенство верно для всех x из 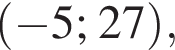 который содержит 31 целое число.
который содержит 31 целое число.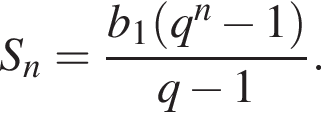 Выразим b1:
Выразим b1: 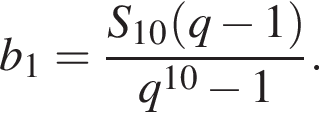 Вспомним, что
Вспомним, что 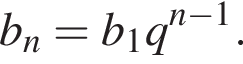
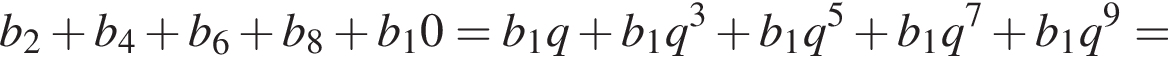
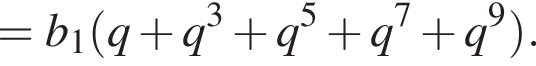
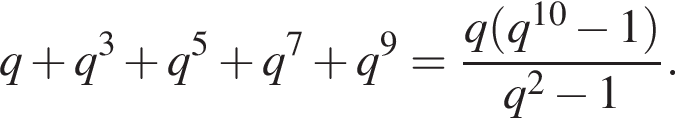 Найдем сумму членов с четными номерами согласно формуле:
Найдем сумму членов с четными номерами согласно формуле: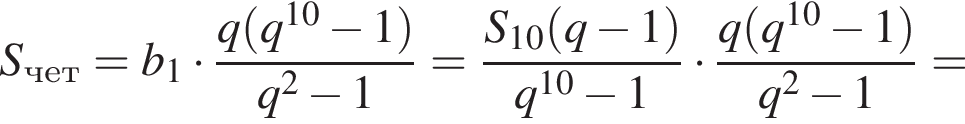
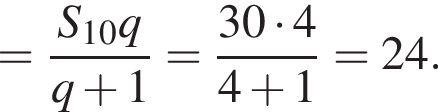
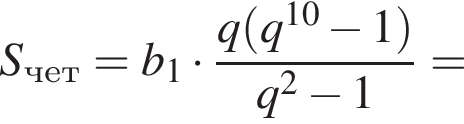
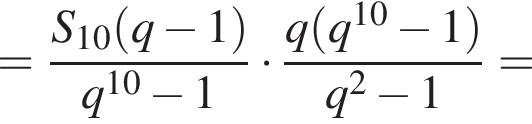
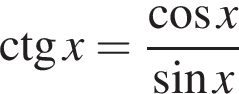 не определена, когда
не определена, когда 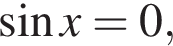 т. е. при
т. е. при 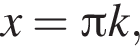 где
где 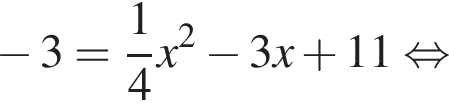
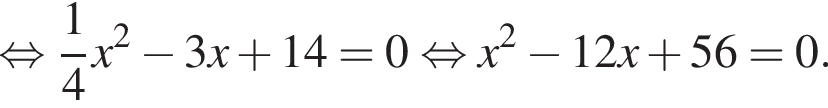
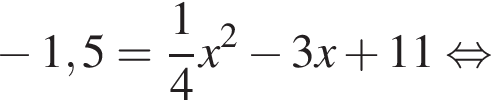
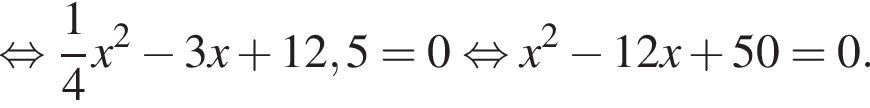
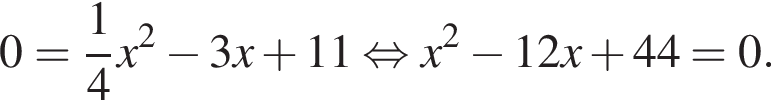 Дискриминант меньше нуля, поэтому пересечений нет.
Дискриминант меньше нуля, поэтому пересечений нет.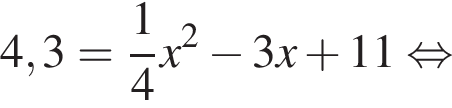
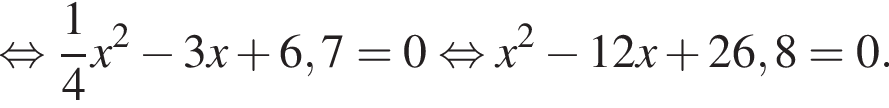
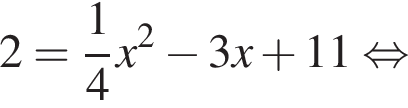
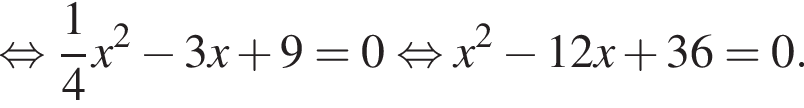
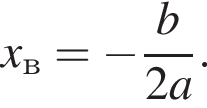 Поэтому
Поэтому 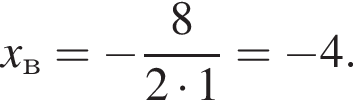 Поскольку y(xв) = −5, имеем:
Поскольку y(xв) = −5, имеем: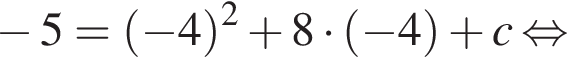

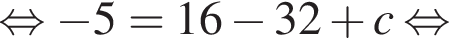
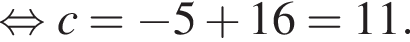
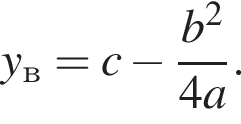
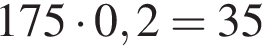 л краски. Можно купить 3 банки по 10 литров и 2 банки по 2,5 литра, тогда минимальная сумма составит:
л краски. Можно купить 3 банки по 10 литров и 2 банки по 2,5 литра, тогда минимальная сумма составит: 